Outlook Report
Executive Summary
Thank you to the groups that contributed to the 2017 SIO reports. For August we received 37 contributions for pan-Arctic extent predictions, nine of which also contributed Alaska regional extent predictions and 10 of which also contributed for Antarctica. We received two additional contributions for Antarctica only and two descriptive regional contributions. This August Outlook report and current conditions were coordinated by lead author Uma Bhatt (University of Alaska Fairbanks) with contributions from Edward Blanchard-Wrigglesworth (University of Washington), François Massonnet (Université catholique de Louvain and Barcelona Supercomputing Center), and the SIPN Leadership Team.
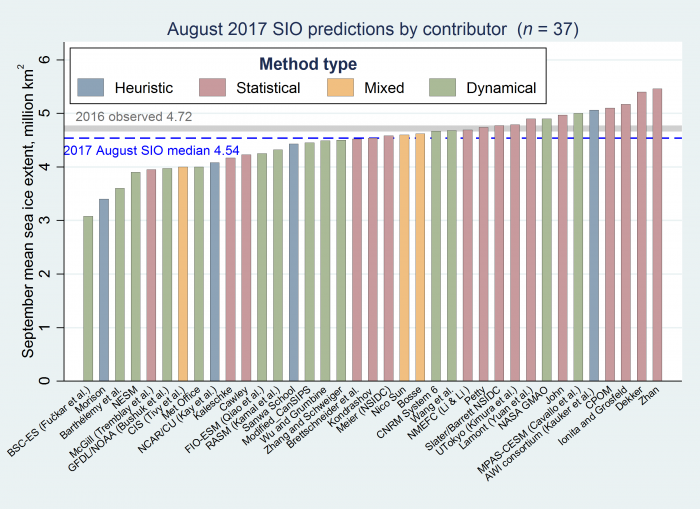
For the August Report there were 37 contributions with the median Outlook value for September 2017 Arctic sea ice extent of 4.5 million square kilometers with quartiles of 4.2 and 4.8 million square kilometers (See Figure 1 in the Overview section, below). These values are unchanged from the July Report, which is consistent with the moderating impact of summer 2017 Arctic weather. The range is 3.1 to 5.5 million square kilometers in August, unchanged from the July Outlook. To place this Outlook in context, recently observed values were 4.3 million square kilometers in 2007, 3.6 million square kilometers in 2012, and 4.7 million square kilometers in 2016. Contributions are based on multiple methods: statistical, dynamical models, heuristic, and mixed. In the June Report the two largest values were from a dynamical model, while the four largest values in July as well as August came from statistical methods. Of interest is that the heuristic approach, influenced by initial low May sea ice extents, continues to have the lowest median value among the various methods. Two participants state that a new record low is likely, though several others suggest it is possible.
Discussion in the section addressing current conditions highlights the record low sea ice in winter of 2017 and early summer (since May) sea ice extents that were similar, and slightly above, the previous low record in 2012. Atmospheric air temperatures and lower sea level pressures were not favorable for rapid sea ice loss between June and early August 2017. Forecasted atmospheric weather conditions continues to be less favorable for major sea ice loss. While one may expect less summer sea ice if the winter ice cover is thin, the summer weather conditions play a dominant role in determining the September minimum.
Please note: The Sea Ice Outlook provides an open process for those interested in Arctic sea ice to share predictions and ideas; the Outlook is not an operational forecast.
Overview
Arctic Outlook contributions are based on multiple methods: statistical, dynamical models, estimates based on trends, and subjective information (Figure 1). This August there were 4 heuristic contributions, 3 mixed contributions that rely on a combination of statistical approaches and heuristic assessment, 15 contributions using statistical methods, and 14 using dynamical models. Fully-coupled models simulate all of the major components of the climate system—including ice, ocean, atmosphere, and land—and allow these component model variables to vary and interact together within the model.
Summary statistics (median; first and third quartiles) for contributions of each method type are given below (in millions of square kilometers):
| Method 2017 | Med | Q1 | Q2 | N |
|---|---|---|---|---|
| Heuristic | 4.3 | 3.7 | 4.7 | 4 |
| Statistical | 4.8 | 4.5 | 5.0 | 16 |
| Mixed | 4.6 | 4 | 4.6 | 3 |
| Dynamical | 4.4 | 4.0 | 4.7 | 14 |
| All | 4.5 | 4.2 | 4.8 | 37 |
The data set is available here.
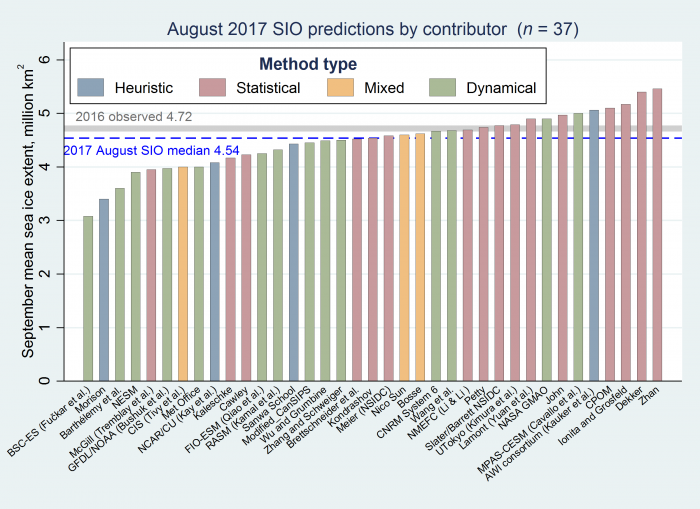
The lowest forecast value comes from a coupled climate model (EC-Earth2.3), which was not bias-corrected. The second lowest value is from a heuristic contribution agrees with the July report and this contribution considered the amount of multiyear ice over the winter of 2016/2017 together with the mean winter atmospheric circulation pattern. The four highest forecasts are statistical, similar to the the July forecast.
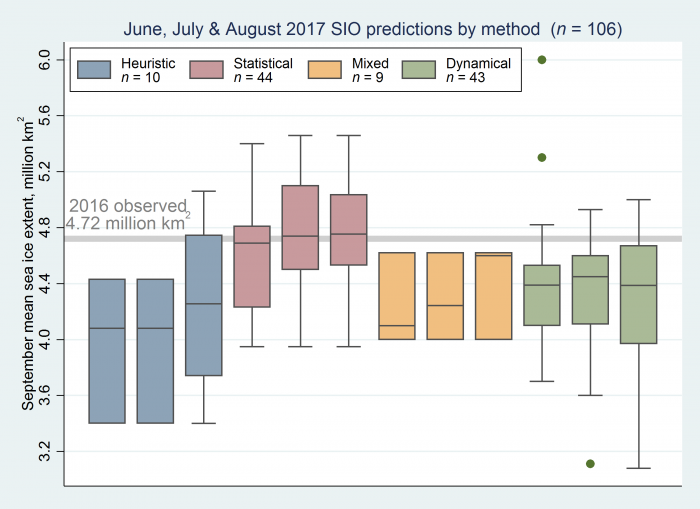
The distribution plot of Outlooks by method (Figure 2) shows the mixed and heuristic estimates are below the overall median of 4.5 million square km while statistical methods are slightly above the overall median. Outlooks from statistical and dynamical models have a considerable range within their respective categories and are below the overall median, consistent with the large number of members for these methods (i.e., n=43).
Comments on Regional Observations
Druckenmiller and Eicken reported in June that ice concentration in the Beaufort Sea is well below normal but over 20% greater than the extreme anomalous conditions during 2016. Note 1998 and 2016 display similar values and had the lowest sea ice concentration areas in the Beaufort Sea over the 1979-2017 period. Multi-year ice is low to completely lacking in the Beaufort Sea. More details provided in the full contribution under the "Individual Outlook PDFs" section at the end of this report.
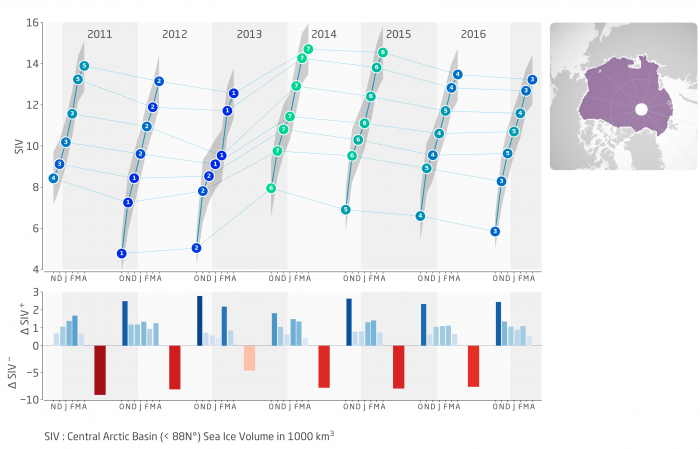
The AWI Cryosat-2 team reported in July they find an ongoing decline of sea ice volume for the past 4 years, where 2017 marks only the 3rd lowest volume of the CryoSat-2 data record (starting in 2011) in the central Arctic basin (Figure 3). This analysis region is limited to exclude areas where the snow climatology is invalid or the sea-ice thickness retrieval data coverage is incomplete. Below average thicknesses in the Chukchi/Beaufort Sea and multiyear ice region as well as above average thicknesses between the North Pole and the Chukchi Sea, and north of Spitsbergen, contribute to the 2017 volume result. More details provided in the full contribution under the "Individual Outlook PDFs" section at the end of this report.
Comments on Predicted Spatial Fields
This month we have received 6 forecasts of September Sea Ice Probability (SIP) (Figure 4). SIP is defined as the fraction of ensemble members in an ensemble forecast with September ice concentration in excess of 15%. All 6 groups submitted June and July SIP forecasts, allowing us to consider the tendency in SIP forecasts and how inter-model spread has evolved. Overall, August SIP forecasts are similar to June and July's forecasts, but the models are slowly converging to a common forecast. Most models tend to forecast a tongue of sea ice in the East Siberian Sea. Nevertheless, there is still considerable SIP forecast uncertainty across models in the Eastern Beaufort Sea, and north of the East Siberia, Kara and Barents Seas (Figure 5). The prospect of an open Northeast Passage (Northern Sea Route) along the Siberian coast is high (mean SIP below 20%), although uncertainty in the SIP forecast for this region has not decreased noticeably through the forecast period. The Northwest Passage is unlikely to open due to significant multi-year ice in the Canadian Archipelago (S. Howell, Environment Canada, personal communication).
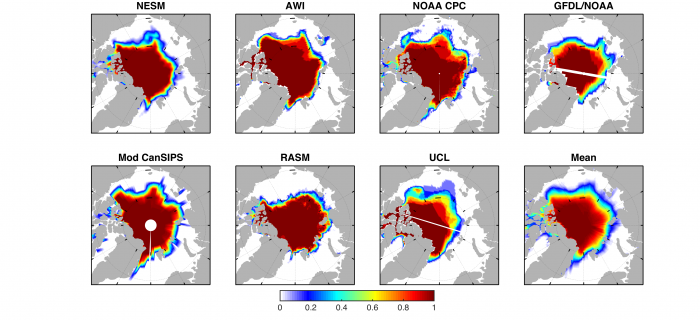
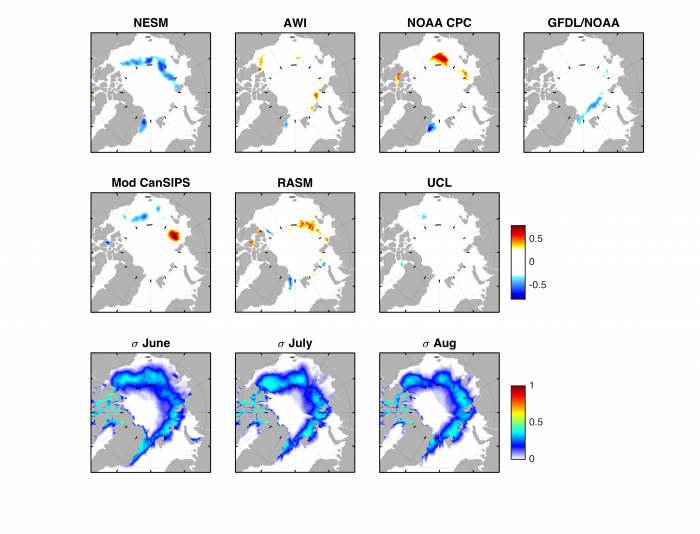
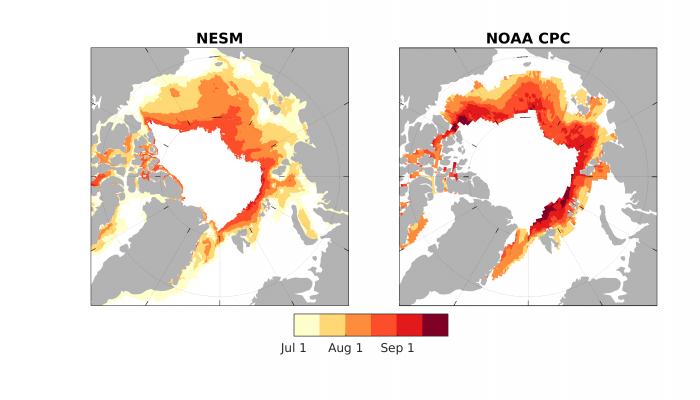
Figure 6 shows the forecasts for Ice Free Day (IFD). IFD is the date in the melt season at which the ice concentration at a given location first drops below 15%. Two models submitted July IFD forecasts: NESM and NOAA CPC. While both models forecast similar patterns of IFD, IFD forecasts by NOAA CPC are a few weeks later than NESM's forecasts.
Current Conditions
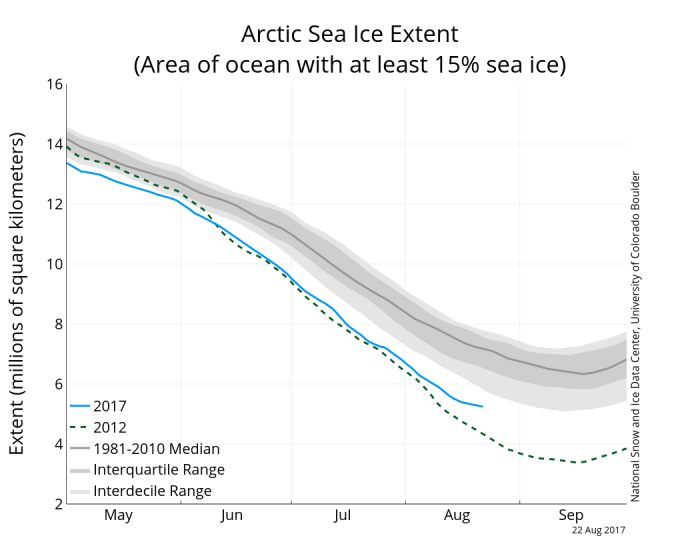
As noted in the June and July SIO Reports, the winter preceding the 2017 summer melt season was the most extreme low in terms of sea ice extent in the satellite record starting in 1979, leading to well-below average extent through the 2016/2017 ice-growth season. The maximum extent for 2017 was the lowest on record, below previous record low maximums in 2016 and 2015. Low winter ice extents were a result of a much warmer winter than average, with greatly reduced total freezing degree days as shown in the June SIO Report.
Ice retreat was normal during the months of May through July for the Arctic as a whole, due to a large region of low sea level pressure (SLP) over the central Arctic basin, which is less favorable for rapid sea ice loss. A key point is that 2017 had been nearly keeping pace with what happened in 2012, the record low sea ice extent year (Figure 7). There is more divergence in early August, and in the past week the ice retreat has slowed considerably; this means that forecasts starting from the end of July may likely end up being lower than the actual September extent.
Sea ice concentration for 22 August shows major open water north of Alaska, and the Chukchi and east Siberian Seas, a continuation of early opening starting in May (Figure 8). The Kara Sea had considerably more open water in July than June, but has stabilized during early August.
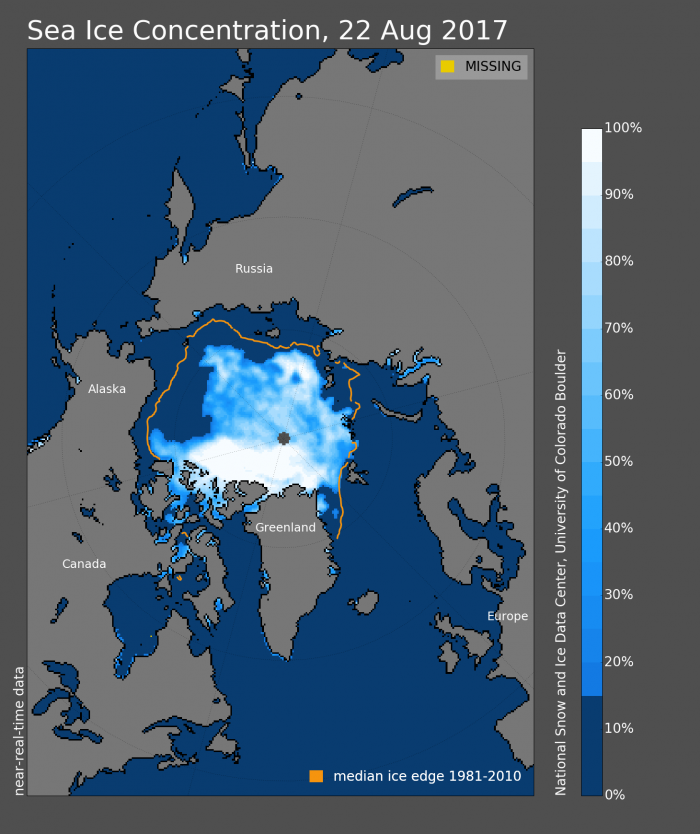
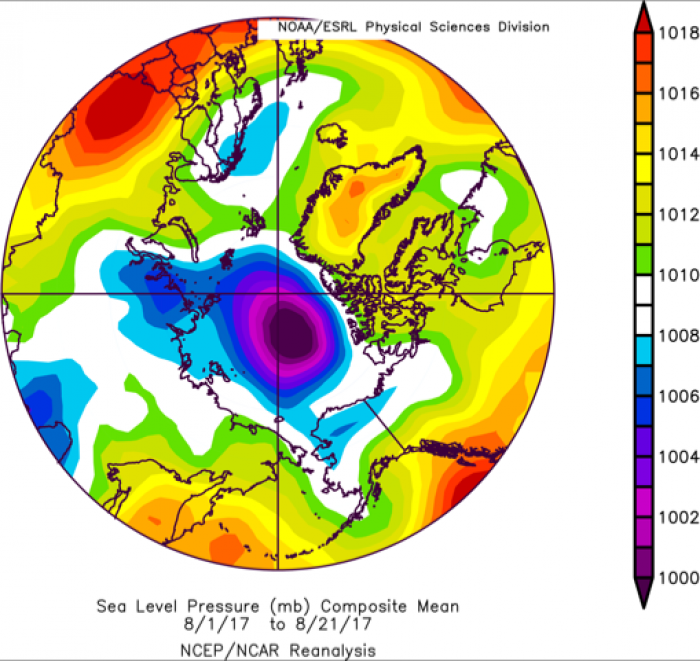
Recent sea ice conditions continue to be dominated by low sea level pressure (SLP) from 1-20 August (Figure 9); note that winds follow the direction of SLP contours, with winds flowing clockwise around high pressure centers and counterclockwise around lows. The central Arctic low SLP keeps colder air circulation within the Arctic basin. Low pressure is typically associated with cloud cover, which reduces solar warming at the surface during the peak summer months. Air temperature anomalies for the same period (not shown) are neutral to slightly negative over most of the Arctic Ocean except for a region in the Canadian Archipelago. The extended range forecast from NOAA/CPC for the end of August 2017 anticipates a continued low pressure pattern over the central Arctic (http://www.cpc.ncep.noaa.gov/products/predictions/814day/814day.03.gif), suggesting a continuation of only modest sea ice melt back in coming weeks due to atmospheric advection.
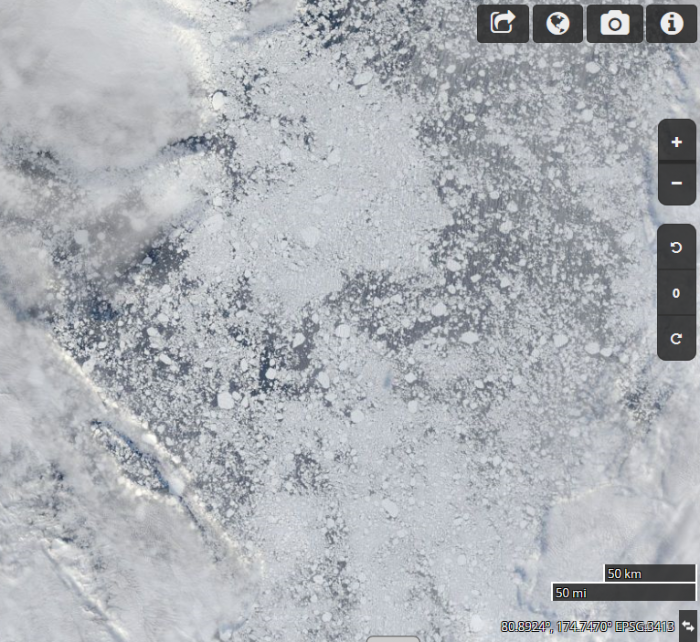
Of concern from the concentration plot (Figure 9), rather than extent, are the extensive regions below <60 %. One should be cautious of summer microwave concentration values, but high resolution imagery supports the diffuse conditions (Figure 10). September 2016 showed diffuse sea ice within the central pack and a similar situation is setting up now. PIOMAS also shows near record low sea ice volumes for July. There are about three weeks left until the date of the sea ice minimum with additional melting expected as a result of a warm ocean. One should be watching interior pack conditions as well as the extent.
Alaska Regional Extent
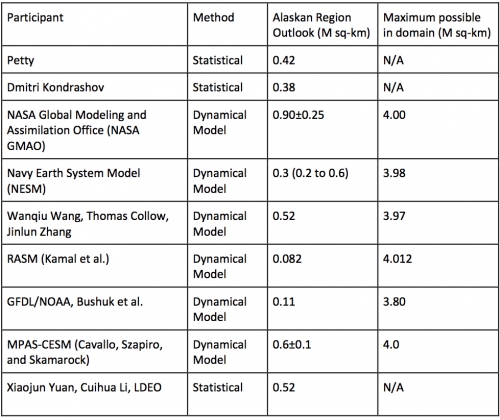
We received nine Alaskan regional Outlooks (combination of the Bering, Chukchi, and Beaufort seas) this month. The median Outlook is 0.42 million square kilometers and the standard deviation is 0.25 million square kilometers. The statistical methods yielded a slightly larger (0.44 versus 0.42) mean than the dynamical methods. The size of the Alaskan region varies slightly among the different participant contributions as a function of the specific forecast-system grids. The average region has an area of 3.96 million square kilometers, so the mean fractional coverage of the Outlooks is about 12% for the month of September.
Antarctic Contributions
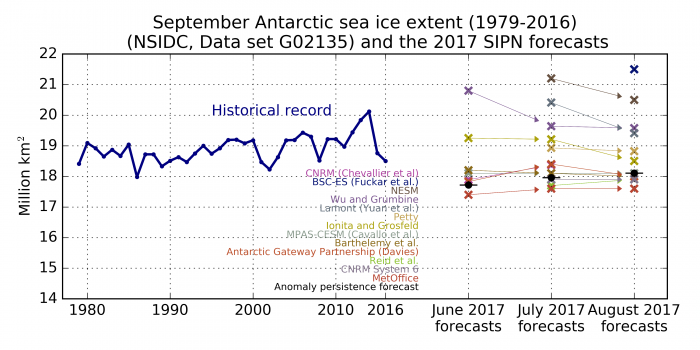
Thanks to the groups that contributed August Antarctic outlooks. We received 12 submissions including one from a new contributor (BSC-ES). As usual, we place caution on the interpretation of the results, as the total September Antarctic sea ice extent is a rather crude metric to evaluate forecast skill. In addition, we do not have hindcast skill information from the systems participating to the exercise.
The spread of contributions that participated to the June, July, and August exercises has decreased as we approached the target month of September. New submissions collected in the meantime have, however, maintained the spread at levels higher than the historical range (Figure 11). We interpret this as a sign that individual forecast systems become more confident as they get closer to the prediction target, but also that model error is a dominant source of uncertainty in Antarctic outlooks. Note however that post-processing is not done consistently across all submissions. For example, BSC-ES submitted raw values (not corrected for the mean bias), which could explain its position as an outlier in the ensemble.
Three forecasts out of 12 suggest a record low maximum for this year (Figure 11). A simple anomaly persistence forecast suggests lower than normal extent, but not a record. Although this is not shown on the figure, the uncertainty in individual predictions is generally large, with values ranging from 0.9 to 1.7 million square kilometers. For comparison, the range of the historical record is 2.14 million square kilometers and the range of the ensemble is 3.9 million square kilometers.
Key Statements/Executive Summaries From Individual Outlooks
The pan-Arctic Outlooks are listed below in order of lowest to highest predicted September extent. Extent and uncertainty (in parentheses) values are provided below in units of millions of square kilometers unless noted otherwise. All individual outlooks can be downloaded as PDFs at the bottom of this webpage. Note that regional, pan-Antarctic, and informal contributions do not have key statements, but are available as PDFs below.
BSC-ES (Fučkar et al.), 3.08 (2.66,3.37), Dynamic Model. We produced September 2017 forecast of Arctic and Antarctic sea ice conditions using coupled climate model (EC-Earth2.3) initialized on May 1st, 2017. This state-of-the-art coupled general circulation model includes dynamic-thermodynamics model of sea ice, LIM2, embedded in NEMO2 ocean model with horizontal resolution of about 1 degree (ORCA1L42). We employ a coupled dynamical model for seasonal forecast because it has capability to resolve and predict many key aspects of global sea ice cover in non-stationary and physically consistent manner.
Morison, 3.4 (+/- 1), Heuristic. (Same as June and July) My June 2017 projection is for a new record low average September, 2017 Arctic sea ice extent of 3.4 million square kilometers. This heuristic estimate is based on what must be the worst pack ice conditions entering the summer season, namely: A) Analysis from Ron Kwok had most of the multiyear ice off Ellesmere Island being swept out of Fram Strait by a persistent low over the central Arctic, and the January 1 multiyear fraction for 2017 was an all time low. The total ice volume must be at a record low for this time of year. B) Temperatures over the Atlantic side of the Arctic Ocean up to the Pole were reportedly warm in late 2016 into early 2017. C) High winter AO should negatively correlate with following September ice extent [Rigor et al., 2002]. Winter (NDJFMA) 2016-17 AO was 9th highest since 1950 and 1.1 above the 1950-88 average. This should influence to ice extent negatively. As always, everything ultimately depends in the summer’s weather, but the ice initial conditions starting the summer melt must be the worst ever so I’m predicting a new record minimum September average of 3.4 million square kilometers.
Barthélemy et al., 3.6 (2.3,4.1), Dynamic Model. Our estimate is based on results from ensemble runs with the global ocean-sea ice coupled model NEMO-LIM3. Each member is initialized from a reference run on July 31, 2017, then forced with the NCEP/NCAR atmospheric reanalysis from one year between 2007 and 2016. Our final estimate is the ensemble median, and the given range corresponds to the lowest and highest extents in the ensemble.
NESM, 3.9 (3.7, 4.4), Dynamic Model. (Same as July) The projected Arctic minimum sea ice extent from the Navy’s global coupled atmosphere-ocean-ice modeling system (Navy Earth System Model - NESM) is 3.9 million square kilometers. This projection is the average of an 11 member ensemble. The range of the ensemble is 3.7 to 4.4 million square kilometers. Note that our ensemble range may not represent a full measure of uncertainty, and the system is currently in a development stage.
McGill (Tremblay et al.), 3.95 (RMSE = 0.472), Statistical. (Same as June and July) We are studying predictability of sea ice in the Arctic Ocean, with a focus on improving our understanding of predictability on a seasonal timescale. To this end we take approaches entirely based on observations. We are interested in the preconditioning effect that winter sea ice dynamics has on the following summer melt. Williams et al (2016) showed that anomalous Fram Strait sea ice export during winter accounts for roughly 40% of the interannual variability of the September sea ice extent (SIE). We use the DJFMA Arctic Oscillation (AO) index as a predictor variable as a proxy for the Fram Export. The DJFMA AO index is significantly correlated with the winter Fram Strait export anomaly (r=0.55) as well as the monthly mean September SIE anomaly (r =-0.51). We have been following the reports of the Sea Ice Outlook as it is the most comprehensive evaluation of the skill of the sea ice prediction community in predicting the September SIE. We are submitting a forecast this year to add to the number of contributors and to see how we perform alongside other types of predictions.
GFDL/NOAA (Bushuk et al.), 3.97 (3.39,4.50), Dynamic Model. Our August 1 prediction for the September-averaged Arctic sea-ice extent is 3.97 million square kilometers, with an uncertainty range of 3.39-4.50 million square kilometers. Our prediction is based on the GFDL-FLOR ensemble forecast system, which is a fully-coupled atmosphere-land-ocean-sea ice model initialized using a coupled data assimilation system. Our prediction is the bias-corrected ensemble mean, and the uncertainty range reflects the lowest and highest sea ice extents in the 12-member ensemble.
CIS (Tivy et al.), 4 , Mixed. (Same as July) Environment Canada’s Canadian Ice Service (CIS) is predicting the 2017 minimum Arctic sea extent at 4.0* 106 square kilometers . As with previous CIS contributions, the 2017 forecast was derived by considering a combination of methods: 1) a qualitative heuristic method based on observed end-of-winter Arctic ice thickness/extent, as well as winter surface air temperature, spring ice conditions and the summer temperature forecast; 2) two simple statistical methods based on an Optimal Filtering Based Model (OFBM), that uses an optimal linear data filter to extrapolate the September sea ice extent time-series into the future and 3) a Multiple Linear Regression (MLR) prediction system that tests ocean, atmosphere and sea ice predictors.
Met Office, 4 (+/-0.8), Dynamic Model. Due to large biases that develop in our model when initializing with July data, our August submission will remain unchanged from the July submission. Nevertheless, by using bias correction methods, we can confirm that our outlook would remain relatively unchanged from both the June and July submissions, however important spatial information would be lost in this process. Using the Met Office GloSea5 seasonal forecast systems we are issuing a model based mean Northern Hemisphere September sea ice extent outlook of (4.0 +/- 0.8) million sq. km. This has been assembled using startdates between 30 May and 19 June to generate an ensemble of 42 members. The Southern Hemisphere September sea ice extent outlook using the same start dates is (17.6 +/- 0.7) million sq. km.
NCAR/CU (Kay et al.), 4.08 (3.10,5.09), Heuristic. (Same as June and July) An informal pool of 30 climate scientists in early June 2017 estimates that the September 2017 ice extent will be 4.08 million sq. km. (std. dev. 0.48, min. 3.10, max. 5.09). Since its inception in 2008, the NCAR/CU sea ice pool has easily rivaled much more sophisticated efforts based on statistical methods and physical models to predict the September monthly mean Arctic sea ice extent (e.g. see appendix of Stroeve et al. 2014 in GRL doi:10.1002/2014GL059388 ; Witness the Arctic article by Hamilton et al. 2014.) We think our informal pool provides a useful benchmark and reality check for Sea Ice Prediction efforts based on more sophisticated physical models and statistical techniques.
Kaleschke, 4.17 (+/-0.5), Statistical. I provide a statistical estimate for the September sea ice extent based on the PIOMAS July thickness: 4.2 +- 0.4
Cawley, 4.23 (+/-1.14), Statistical. (Same as June and July) This is a purely statistical method (Gaussian Process, related to Kriging) to estimate the long-term trend from previous observations of September Arctic sea ice extent. As this uses only September observations, the prediction is not altered by observations made during the Summer of 2016.
FIO-ESM (Qiao et al.), 4.25 (+/-0.46), Dynamic Model. Our prediction is based on FIO-ESM (the First Institute of Oceanography-Earth System Model) with data assimilation. The prediction of September pan-Arctic extent in 2017 is 4.25 (+/-0.46) million square kilometers. 4.25 and 0.46 million square kilometers are the average and one standard deviation of 10 ensemble members, respectively.
RASM (Kamal et al.), 4.323 (+/- 0.1354), Dynamic Model. We used the Regional Arctic System Model (RASM), which is a limited-area, fully coupled climate model consisting of the Weather Research and Forecasting (WRF) model, Los Alamos National Laboratory (LANL) Parallel Ocean Program (POP) and Sea Ice Model (CICE) and the Variable Infiltration Capacity (VIC) land hydrology model (Maslowski et al. 2012; Roberts et al. 2014; DuVivier et al. 2015; Hamman et al. 2016; Hamman et al. 2017; Cassano et al. 2017). WRF and VIC are configured on the same polar stereographic grid at 50-km resolution, and POP and CICE are sharing a rotated spherical grid at 1/12o (~9 km). Reanalysis data are used to force RASM from September 1979 to August 2017, after that the NCEP version 2 Coupled Forecast System model (CFSv2) Operational Forecasts are used for forecast forcing.
Sanwa School (Citizen Scientist/Public), 4.43 , Heuristic. (Same as June and July) Monthly mean ice extent in September will be about 4.43 million square kilometers. We estimated the minimum ice area through discussion among 21 students based on the ice map from 2004 to 2016.
Modified_CanSIPS, 4.45 (+/-0.37), Dynamic Model. Our forecasts of total Arctic sea ice extent (SIE) and sea ice probability (SIP) were produced using the Canadian Seasonal to Interannual Prediction System (CanSIPS), but in a modified experimental mode intended to test several potential updates to the sea ice forecast methodology. These updates include changes to the data used to initialize both sea ice concentration (SIC) and sea ice thickness (SIT), as well as the methodology to produce probabilistic SIC forecasts.
Wu and Grumbine, 4.49 (3.00, 5.51), Dynamic Model. The projected Arctic minimum sea ice extent from the NCEP CFSv2 model with revised CFSv2 May-July initial conditions (ICs) using 92-member ensemble forecast is 4.49 million square kilometers with a standard deviation (SD) of 0.65 million square kilometers.
Zhang and Schweiger, 4.5 (+/-0.5), Dynamic Model. Driven by the NCEP CFS forecast atmospheric forcing, PIOMAS is used to predict the total September 2017 Arctic sea ice extent as well as ice thickness field and ice edge location, starting on August 1. The predicted September ice extent is 4.5± 0.5 million square kilometers.
Brettschneider et al., 4.52 (3.99,5.29), Statistical. (Same as July) Forecast is based on an analog method. The analogs are based on sea level pressure, air temperature, sea surface temperature and upper-air geopotential height over several domains within (and including the entire) Northern Hemisphere. The September sea ice extent, expressed as a departure from the 1979-2016 trend line, is the predicted quantity. The actual prediction is the mean September pan-Arctic ice extent of the five best analog years.
Kondrashov , 4.54 , Statistical. This contribution relies on data-harmonic analysis techniques to predict sea ice conditions over the Pan-Arctic region. The prediction model is obtained by data-adaptive harmonic decomposition and stochastic inverse modeling of Multisensor Analyzed Sea Ice Extent – Northern Hemisphere (MASIE-NH) dataset, as well as regional sea ice extent (SIE) from Sea Ice Index (SII) dataset.
Meier (NSIDC), 4.58 (std. dev. 0.43), Statistical. This method applies daily ice loss rates to extrapolate from the start date (July 31) through the end of September. Projected September daily extents are averaged to calculate the projected September average extent. Individual years from 2005 to 2016 are used, as well as averages over 1981-2010 and 2005-2016. The 2005-2016 average daily rates are used to estimate the official submitted estimate. The predicted September average extent for 2017 is 4.58 (±0.43) million square kilometers. The minimum daily extent is predicted to be 4.47 (±0.43) million square kilometers and occur on 17 September. These values are lower than the July submission (September average of 4.52 [±0.63] million square kilometers and minimum daily extent of 4.41 [±0.62] million square kilometers). The range (standard deviation) is substantially smaller than the July submission, but still indicates substantial variability in ice loss rates over the final ~1.5 months of the melt season. Based on the last 12 years, there is only a minimal chance that 2017 will be lower than the current record low extent of 2012.
Nico Sun (Citizen Scientist/Public), 4.6 (4.3,4.87), Mixed. The forecast model is based on a global surface radiation model and uses arctic albedo to calculate daily sea ice area and volume losses. The average error for the hind-cast (2007-2016 period) is 0.147 million square kilometers for daily minimum sea ice area. In the future it will be used as a reference for machine learning forecasts.
Bosse (Citizen Scientist/Public), 4.62 (+/-0.45), Mixed. (Same as June and July) Just as in the last years my guess is derived from the 0...700m OHC of the Atlantic part of the arctic. For the detailed mapping of the data from Argo and the physical explanation see here. The average of the monthly June...September OHC-data of the year n is the input for a linear regression to estimate the september mean of the sea ice extent for the year n+1. In this year I do not consider the PIOMAS- data due to some doubts of the validity of this model in the light of the Cryosat data.
CNRM System 6, 4.67 (3.92,5.32), Dynamic Model. (Same as July) This second CNRM outlook has been run with Meteo France system 6. This pre-operational system is based on a new version of CNRM global climate model, CNRM-CM6, and on new ocean-sea ice initial conditions produced by Mercator Ocean. The system used to produce this outlook differs with the other ("CNRM") with respect to (i) model horizontal and vertical resolution (ii) model physics in the atmosphere and ocean and (iii) new initial conditions.
Wang et al., 4.68 (+/- 0.16), Dynamic Model. The outlook is calculated 0.5X0.5 grid output. The outlook is from CPC experimental dynamical ensemble forecast. The ensemble includes 20 forecast members.
NMEFC (Li & Li ), 4.69 , Statistical.(Same as July) We predict the September monthly average sea ice extent of Arctic by statistic method and based on monthly sea ice concentration and extent from National Snow and Ice Data Center. The result shows that the Sep. ice extent will be less slightly in 2017 than in 2016.
Petty, 4.74 , Statistical. Based on an analysis of June sea ice concentration data provided by the NSIDC (NASA Team), I forecast a 2017 September Arctic sea ice extent of 4.50 +/- 0.35 M square kilometers. This is slightly lower than the May forecast, and instead is very similar to the extent expected from persistence of the long-term linear trend. The forecast does not suggest a new record low September extent will be reached in 2017 (lower than the 3.62 M square kilometers observed in 2012). The June forecast appear to be driven primarily by the low SIC in the Beaufort and Laptev seas. Our June forecast of Alaskan sea ice extent is coming in at 0.37 M square kilometers, so slightly lower than the May forecast (0.41). We also produced, for the first time, an Antarctic September sea ice forecast using the same methodology. This does show some skill, especially in more recent years (since 2008). The forecast is 18.93 M square kilometers.
Slater/Barrett NSIDC, 4.77 , Statistical. This projection was made using the Slater Probabilistic Ice Extent model developed by Drew Slater. The model computes the probability of sea ice concentration greater than 15% for Arctic Ocean grid cells in the EASE 25 km grid. These probabilities are aggregated over the model domain to arrive at daily ice extents. A September mean ice extent is calculated from daily forecasts issued on August 1. While the model has predictive skill at lead times up to 90 days, NSIDC runs the forecast model with a 50 day lead time. Forecasts issued on August 1 for September have lead times spanning 32 to 61 days. Therefore we consider the mean September ice extent forecast for the August sea ice outlook to have more skill than forecasts issued in June or July.
UTokyo (Kimura et al.), 4.79 , Statistical. (Same as July) Monthly mean ice extent in September will be about 4.79 million square kilometers. Our estimate is based on a statistical way using data from satellite microwave sensor. We used the ice thickness in December and ice movement from December to May. Predicted ice concentration map from July to September is available in our website. Sea ice in the Laptev Sea and Chukchi Sea is expected to be thin and retreat quickly. On the other hand, sea ice in the East Siberian Sea will retreat slowly with nearly same speed as normal years. On the Canadian side, sea ice in the Beaufort Sea is expected to be thick and retreat slowly compared with the last year.
Lamont (Yuan et al.), 4.9 (RMSE = 0.33), Statistical. A statistical model, namely linear Markov model, is used to predict monthly Arctic sea ice concentration (SIC) at all grid points in the pan Arctic region. The model is built in a multi-EOF space and is capable to capture the co-variability in the ocean-sea ice-atmosphere system. The September pan Arctic sea ice extent (SIE) is calculated from predicted SIC. The model predicts negative SIC anomalies throughout the pan Arctic region. These anomalies are relative to the 1979-2012 climatology. The September mean pan Arctic SIE is predicted to be 4.90 million square kilometers with an RMSE of 0.33 million square kilometers. Similar statistical models were also developed to predict the SIE in the Alaskan region and the SIE in the Antarctic. The September mean pan Antarctic SIE is predicted to be 19.41 million square kilometers with an RMSE of 0.84 million square kilometers. The Alaskan regional SIE is predicted to be 0.52 million square kilometers with an RMSE of 0.20 million square kilometers.
NASA GMAO, 4.9 (std. dev. 0.34), Dynamic Model. An experiment of the GMAO seasonal forecasting system using CryoSat-2 derived ice thickness predicts a September average Arctic ice extent of 4.90 ± 0.34 million square kilometers . The test examines the application of ice thickness data in a near-real time setting for the seasonal forecast system.
John, Christian (Citizen Scientist/Public), 4.971 (+/-0.34), Statistical. My contribution is based on the idea that Temperature of Sea-Surface and Air Temperature(70-90N)can be used to explain most of the Year to Year Variability of September Sea-Ice-Extent,it is able to show that both can work as a proxy for the strength of Extent Melt to September.While Longterm-Trend is mainly caused by human induced climate change, it herefore argue that the Year to Year variability can explained by Temperature-Variability
MPAS-CESM (Cavallo et al.), 5 (std. dev. 0.6), Dynamic Model. (Same as July) Our August 1 predictions are the means and standard deviations from an ensemble of forecasts from July 31st using MPAS-CESM as a fully-coupled atmosphere-land-ocean-sea ice model. The control member is initialized from GFS analysis for the atmosphere and a restart from member 20 of the CESM Large Ensemble for the other components. An 11 member initial condition ensemble is constructed in 2 sets: a perturbed atmosphere (GEFS members 1-5) and perturbed other components (with Large Ensemble members 5-9).
AWI Consortium (Kauker et al.) , 5.06 (std. dev. = 0.27), Heuristic. (Same as July) Sea ice-ocean model ensemble prediction initialised with assimilation of sea ice and ocean observations.
CPOM, 5.1 (+/-0.5), Statistical. (Same as July) Based on melt pond fraction in May+June we predict a mean 2017 September ice extent of 5.1 (4.6 to 5.6) million square kilometers (within the range observed during last 4 years). The likelihood for a new record minimum is below 1%. While melt pond fraction has been above 2006-2015 mean values in the western parts of the Arctic, less ponding and melting occurred in the eastern part due to more snow and relatively cold temperatures. In the past the regions - where melt pond fraction is low in 2017 - were more important for September ice extent than e.g. the Beaufort Sea. Consequently, we predict the September ice extent to be quite large in spite of the lowest Arctic ice volume in recent months.
Ionita and Grosfeld, 5.17 (4.81,5.54), Statistical. Sea ice in both Polar Regions is an important indicator for the expression of global climate change and its polar amplification. Consequently, a broad information interest exists on sea ice, its coverage, variability and long term change. Knowledge on sea ice requires high quality data on ice extent, thickness and its dynamics. As an institute on polar research we collect data on Arctic and Antarctic sea ice, investigate its physics and role in the climate system and provide model simulations on different time scales. All this data is of interest for science and society. In order to provide insights into the potential development of the seasonal signal, we developed a robust statistical model based on ocean heat content, sea surface temperature and atmospheric variables to calculate an estimate of the September minimum sea ice extent for every year.
Dekker (Citizen Scientist/Public), 5.4 (+/- 0.342), Statistical. (Same as July) My projection is based on an estimate of how much heat the Northern Hemisphere absorbs during spring and early summer. I use three variables (land snow cover, ice concentration, ice area) that are available in June, in a formula which shows particularly strong correlation with Sept sea ice extent. Regressed over the 1992 - 2015 period, the formula projects 4.1 M square kilometers for September 2016, with a standard deviation of only 340 k square kilometers. Past performance of this June forecast method for September ice extent over the past 24 years shown in a graph here. The interesting finding is that the June land snow cover signal is clearly present in the September ice extent numbers.
Zhan, 5.46 (+/- 0.3), Statistical. (Same as July) We estimated the September sea ice extent in 2017 to be much larger than last year. Compared to June 2016, MISR (firstlook product) indicates a significant increase in RSR over both the Canadian Arctic Archipelago and Svalbard, which consistent with the sea ice concentration anomaly. The area-weighted Pan-Arctic mean June RSR 2017 is much larger than that in 2016 and only slightly smaller than 2014.